1. Introdução
O artigo anterior realizou uma introdução ao problema das “Torres de Hanói” e definiu a classe TorresDeHanoi - que corresponde a uma implementação da solução recursiva clássica do problema em Java. Você pode consultar o artigo através do link://www.devmedia.com.br/post-23738-Torres-de-Hanoi-solucao-recursiva-em-Java.html
O objetivo deste novo artigo é explicar o funcionamento da classe TorresDeHanoi. Basicamente, foi realizada uma transposição direta da solução recursiva para código Java, através da programação de um método recursivo chamado hanoi. O corpo da classe TorresDeHanoi é reproduzido abaixo, com alguns comentários adicionais:
Listagem 1: Classe TorresDeHanoi
public class TorresDeHanoi {
// Método que realiza (imprime) o movimento
// de um disco entre dois pinos
private static void mover(int O, int D) {
System.out.println(O + " -> " + D);
}
// Método que implementa a recursão
// n = número de discos a serem movimentados
// O = atual pino origem
// D = atual pino destino
// T = atual pino de trabalho
static void hanoi(int n, int O, int D, int T) {
if (n > 0) {
hanoi(n - 1, O, T, D); //executa hanoi para mover n-1 discos
//da origem para o trabalho
mover(O, D); //mover disco do "pino O" (origem atual)
//para o "pino D" (destino atual)
hanoi(n - 1, T, D, O); //executa hanoi para mover n-1 discos
//do trabalho para destino
}
}
Listagem 2: Exemplo de chamada
//executa o método recursivo “hanoi”
//move os n discos do pino 1 para o pino 3, usando o pino 2 como auxiliar
TorresDeHanoi.hanoi(n, 1, 3, 2);
2. Explicando a Solução Recursiva
Esta seção apresenta uma explicação passo-a-passo do funcionamento do programa, apresentando a sequência de chamadas recursivas e de movimentos realizados. Será considerado um jogo com 3 discos (ou seja, n = 3). O recurso básico utilizado para a explicação é um diagrama que apresenta a árvore de recursão das chamadas do método “hanoi”. No diagrama, as seguintes convenções foram utilizadas:· Os retângulos azuis indicam o estado (configuração dos parâmetros) de uma chamada ao método “hanoi”. Observe que substituímos o nome do método “hanoi” por “h”, apenas para que desenho não ficasse poluído.
· Uma seta com linha sólida entre dois retângulos consiste em uma chamada recursiva (estas setas estão sempre direcionadas para baixo).
· Uma seta com linha pontilhada entre dois retângulos consiste em um retorno de chamada recursiva (estas setas estão sempre direcionadas para cima).
· Uma seta vermelha apontando para movX->Y indica um movimento do disco do topo do pino X para o topo do pino Y.
· Os números dentro dos círculos amarelos indicam a ordem de execução de cada comando. As chamadas recursivas são prefixadas com a letra “c” e os movimentos de disco com a letra “m”.
O diagrama da árvore de recursão da solução do problema das “Torres de Hanói” com 3 discos é apresentado a seguir:
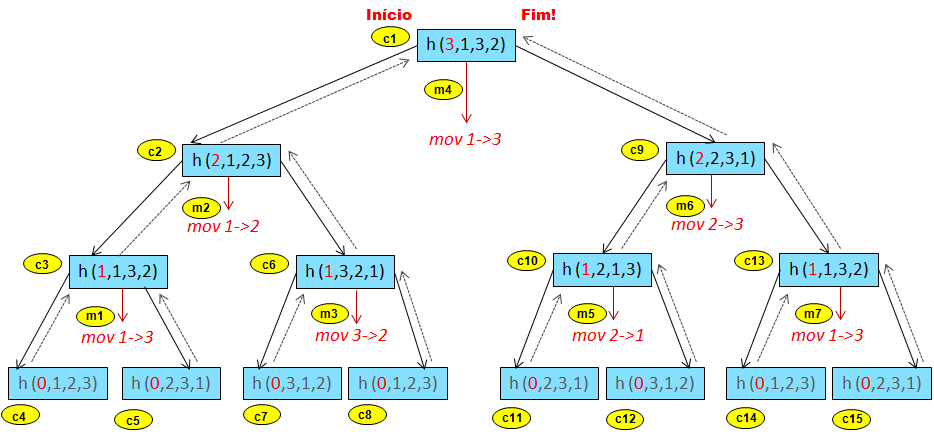
Figura 1
Muitas vezes as pessoas têm dificuldade de compreender programas recursivos. A princípio eles parecem mais complicados, porém, depois que você “pega o jeito” da recursão acaba por perceber que os programas recursivos são normalmente mais simples do que os iterativos. Uma boa forma de compreender a recursão é exatamente a usada neste artigo: simular a execução do programa desenhando uma árvore de recursão. Compare o código Java do método “hanoi” com o esquema apresentado. Para lhe ajudar, será apresentada uma explicação dos primeiros passos executados.
· Início->c1: corresponde à chamada inicial para TorresDeHanoi.hanoi(3, 1, 3, 2), ou seja, resolver o problema da torre com 3 discos, onde o 1 é o “pino origem”, 3 é o “pino destino” e 2 é o “pino de trabalho”. Normalmente essa chamada será feita pelo método main do programa que usará a classe “TorresDeHanoi”.
· c1->c2: Como temos n > 0, então o programa entra no “if” do corpo do método “hanoi” e ocorre a execução do primeiro comando de “c1”, que corresponde a uma chamada recursiva para TorresDeHanoi.hanoi(2, 1, 2, 3). Isso faz com que a “c1” seja empilhado na pilha de chamadas de método.
· c2->c3: mais uma vez n > 0, o que ocasiona a execução do primeiro comando de “c2”, que corresponde a uma chamada recursiva para TorresDeHanoi.hanoi(1, 1, 3, 2). Desta forma, “c2” é empilhado na pilha de chamadas de método.
· c3->c4: novamente n > 0, o que ocasiona a execução do primeiro comando de “c3”, que corresponde a uma chamada recursiva para TorresDeHanoi.hanoi(0, 1, 2, 3). Sendo assim, “c3” é empilhado na pilha de chamadas de método.
· c4->c3: opa! Desta vez n = 0. Com isto, o programa não executa os comandos subordinados ao “if” do corpo do método “hanoi”. Ocorreu a condição de parada da recursão. Nenhum comando da chamada “c4” é executado e a chamada “c3” é desempilhada para que a sua execução prossiga.
· c3->m1: corresponde ao segundo comando da chamada “c3” (que acaba de ser desempilhada). Realiza a execução do movimento de um disco do “pino 1” para o “pino 3”.
· c3->c5: o último comando da execução de “c3” consiste em uma chamada recursiva para TorresDeHanoi.hanoi(0, 2, 3, 1). Sendo assim, “c3” é empilhado na pilha de chamadas de método.
· c5->c3: temos n = 0, a condição de parada da recursão. Nenhum comando da chamada “c5” é executado e a chamada “c3” é desempilhada para que a sua execução prossiga.
· c3->c2: não há mais nenhum comando em “c3”, então “c2” é desempilhado para que a sua execução possa prosseguir.
· c2->m2: corresponde ao segundo comando da chamada “c2” (que acaba de ser desempilhada). Realiza a execução do movimento de um disco do “pino 1” para o “pino 2”.
· E assim a execução prossegue... Não é possível apresentar a relação completa de chamadas e movimentos, pois assim nosso artigo ficaria enorme! Mas o resto da execução segue o mesmo padrão, basta observar o diagrama e seguir as setas!!!
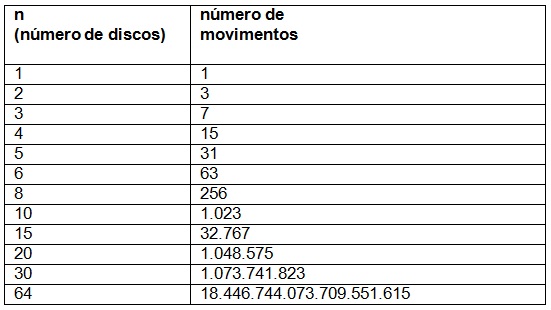
3. Complexidade do Algoritmo
O algoritmo apresentado requer 2^n - 1 movimentos para transferir todos os discos do “pino origem” para o “pino destino”. Diversos livros de matemática e computação provam, através de indução matemática, que este é o número mínimo de movimentos necessários. Considerando o número de passos executados pelo procedimento recursivo, tem-se que a complexidade do mesmo é O(2^n) .A tabela abaixo apresenta o número de movimentos necessários para resolver o problema de acordo com diversos valores do parâmetro n (número de discos).