1. Introdução
Imagine três objetos que chamaremos de ‘A’, ‘B’ e ‘C’. A seguir, relacionamos todas as possíveis maneiras para dispor esses objetos. Em outras palavras, apresentamos todas as formas de permutar os objetos:
- ‘A’, ‘B’ e ‘C’
- ‘A’, ‘C’ e ‘B’
- ‘B’, ‘A’ e ‘C’
- ‘B’, ‘C’ e ‘A’
- ‘C’, ‘A’ e ‘B’
- ‘C’, ‘B’ e ‘A’
Quando estamos desenvolvendo um sistema, é muito comum que nos deparemos com situações práticas em que precisaremos lidar com permutações. Por exemplo: sistemas que lidam com otimização de recursos, normalmente necessitam trabalhar com testes envolvendo permutações para determinar a forma menos custosa de realizar um conjunto de n tarefas.
Neste artigo apresentamos um algoritmo recursivo em Java para implementar a permutação de objetos. O artigo está dividido em duas partes. Na primeira introduzimos um algoritmo básico capaz de gerar e apresentar todas as permutações de n objetos sem repetição. Na segunda mostramos como modificar este algoritmo para que ele possa realizar permutações com repetição de objetos.
2. Permutações sem Repetição: um Algoritmo RecursivoAntes de entramos no algoritmo propriamente dito, vamos abordar a questão do número total de permutações de n objetos. Este número é dado por P(n) = n!. Ou seja: para 3 objetos (como no caso do exemplo apresentado na introdução do artigo), P(3) = 3! = 3 x 2 x 1 = 6 permutações. Para 4 objetos temos: P(4) = 4! = 4 x 3 x 2 x 1 = 24 permutações. Para 10 objetos, o total já chega à casa dos milhões: P(10) = 10! = 3.628.800. Veja que um pequeno aumento no número de objetos resulta em um grande crescimento no total de permutações.
O recurso básico para a elaboração do algoritmo consiste na montagem de uma árvore de recursão mostrando uma “instância” de solução para o problema. Um exemplo é mostrado na figura 1, onde apresenta-se a árvore de recursão considerando a permutação de 3 objetos.
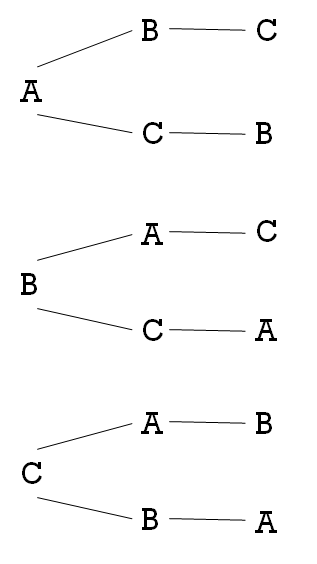
Figura 1: Árvore de recursão da solução do problema das permutações de 3 objetos
A árvore de recursão nos deixa claro que permutar n elementos é uma atividade similar a colocá-los dentro de n gavetas (este é o exemplo típico apresentado nos livros de Probabilidade e Estatística). Se temos 3 objetos e colocamos o objeto ‘A’ na primeira gaveta, então existem duas opções para a segunda gaveta: ‘B’ ou ‘C’. Se ‘B’ for colocado na segunda gaveta, então sobrará apenas a terceira gaveta para ‘C’. E por aí vai! Cada caminho na árvore de recursão corresponde a uma diferente permutação e no exemplo da figura 1 existem 6 caminhos, pois sabemos que P(3) = 6.
A listagem 1 mostra o código Java com a definição da classe “Permutacoes”. Esta classe possui um método público estático chamado “permuta” que recebe um vetor de char como entrada e apresenta todas as formas de permutar os objetos desse vetor.
Listagem 1: Classe “Permutacoes”
/**
* Esta classe gera e imprime as diferentes permutações de n objetos
*
*/
public class Permutacoes {
//numero da permutacao atual
private static int cont=0;
//armazena a permutacao corrente
private static char[] p;
/**
* metodo principal: recebe o vetor cujos elementos que serao permutados
* @param vet
*/
public static void permuta(char [] vet) {
p = new char[vet.length];
permuta(vet,0);
}
/**
* método recursivo que implementa as permutacoes
* @param vet
* @param n
*/
private static void permuta(char []vet, int n) {
if (n==vet.length) {
cont++;
imprime();
} else {
for (int i=0; i < vet.length; i++) {
boolean achou = false;
for (int j = 0; j < n; j++) {
if (p[j]==vet[i]) achou = true;
}
if (!achou) {
p[n] = vet[i];
permuta(vet,n+1);
}
} //--for
} //--if/else
} //--permuta
/** imprime a permutacao corrente */
private static void imprime() {
System.out.println();
System.out.print("(" + cont + ") : ");
for (int i=0; i < p.length; i++) System.out.print(p[i] + " ");
} //--imprime
/** metodo principal para teste da classe */
public static void main(String[] args) {
char v[] = {'A','B','C', 'D'};
Permutacoes.permuta(v);
}
}
Como o programa funciona? Para começar, observe que temos dois vetores:
- “vet”: vetor contendo os objetos que serão permutados.
- “p”: vetor auxiliar que conterá uma permutação sempre que a base da recursão for alcançada (ou seja, sempre que um caminho completo da árvore de recursão for estabelecido).
O método principal da classe é “permut(vet, n)”. Trata-se do método que é chamado recursivamente para gerar as diferentes permutações. Vamos analisar o seu funcionamento. Iniciando do nível n=0 (digamos que este é o nível da primeira gaveta) o método recursivo “permut” executa um laço for que varrerá o vetor “vet” do primeiro ao último elemento. Com isso, um dado objeto será posto na primeira gaveta (que consiste na posição 0 de “p”). Após preencher a primeira gaveta, é feita uma chamada recursiva para “permut”, mas agora passando para o nível n=1 (segunda gaveta). O laço for se encarrega de colocar na segunda gaveta um elemento diferente daquele que está na primeira e, novamente, faz a chamada para “permut”, dessa vez para tratar o nível n = 2 (terceira gaveta). A terceira gaveta deverá conter um objeto diferente dos que foram colocados na primeira e na segunda.
E assim o método segue a sua execução, até que a última gaveta seja preenchida (caso que ocorre quando n == vet.length). Nesse caso, a base da recursão é atingida e podemos realizar a impressão do conteúdo de “permut”.
Para o exemplo onde temos um vetor composto por 4 objetos, o resultado da execução do programa será equivalente ao apresentado na figura 2.

Figura 2: Resultado da execução do programa da listagem 1
3. Permutações com Repetição
A geração de diferentes permutações de objetos é um problema clássico da computação e que possui inúmeras aplicações práticas. Na seção anterior apresentamos a implementação de uma solução recursiva em Java para este problema. É importante observar que o programa trata o caso das permutações sem repetição (permutações que não podem conter objetos repetidos) que é o caso mais comum na prática. No entanto, é bastante simples adaptar o programa da listagem 1 para tratar o caso das permutações com repetição (permutações contendo objetos repetidos como ‘AABC’, ‘ABBB’, ‘CDCD’, etc.) bastando para isso apenas mexer em um pequeno trecho de código do método “permuta(vet,n)”. Sendo mais direto: basta modificar o conteúdo mostrado na listagem 2 pelo mostrado na listagem 3:
Listagem 2: Código que deve ser removido
boolean achou = false;
for (int j = 0; j < n; j++) {
if (p[j]==vet[i]) achou = true;
}
if (!achou) {
p[n] = vet[i];
permuta(vet,n+1);
}
Listagem 3: Código que deve ser colocado
p[n] = vet[i];
permuta(vet,n+1);
Na Figura 3, um exemplo considerando a permutação com repetição de 3 objetos:

Figura 3: Permutação com repetição de 3 objetos
E assim terminamos o artigo! Até a próxima!







