Veja neste artigo como desenvolver, em C#, um programa que utiliza o chamado “Método da Bissecção” para encontrar a raíz aproximada de uma função que geralmente necessitaria de um pouco mais de trabalho para ser resolvida da forma convencional, isolando variáveis e realizando operações aritméticas simples.
De fato este artigo é um pouco diferente dos demais existentes no portal no que se refere ao tema. Resolução de equações não é algo comumente visto no meio de programação, banco de dados ou semelhantes. Este tema é mais comum a estudantes e profissionais de engenharia e áreas das ciências exatas. Porém, não quer dizer que não possa chegar ao conhecimento de todos, não é mesmo? E por isso estou compartilhando com vocês.
Suponha que você é um engenheiro eletricista e se depara com um circuito elétrico cuja corrente i é dada por i = 9e^(-t)cos(2̃πt), onde t é dado em segundos. Você precisa determinar em que instante a corrente no circuito será igual a 3 amperes.
Primeiro vamos organizar as equações, se queremos i=3, temos:
9e^(-t)cos(2̃πt) = 3 à 9e^(-t)cos(2̃πt) - 3 = 0
Essa será nossa função f, da qual buscaremos encontrar a raíz:
f(t) = 9e^(-t)cos(2̃πt) - 3
Para termos uma noção de quanto vale t quando i=3, vamos plotar o gráfico da função. Como falamos em tempo, avaliaremos apenas instantes em que t>=0 (no caso, usaremos t de 0s a 1s) e obteremos os seguinte gráfico:
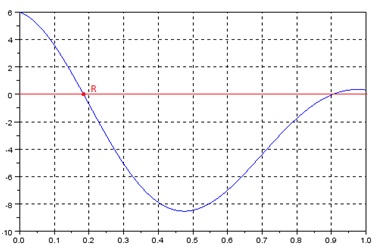
Figura 1. Gráfico da função 9e^(-t)cos(2̃πt) - 3
Observamos que o primeiro instante t em que i=3 está entre 0.1s e 0.2s, mas não temos um valor mais preciso. É aqui que entra o método numérico da bissecção.
Este método tem esse nome por que ele se baseia em intervalos para encontrar uma raiz aproximada de forma iterativa e, a cada iteração, ele secciona o intervalo ao meio, obtendo dois intervalos menores.
Após seccionar o intervalo original, verificamos se a raiz está no primeiro subintervalo ou no segundo. Para fazer essa verificação, analisamos o valor da função no início do intervalo [a,b] e no fim. Se f(a)*f (b)<0 indica que a está antes da raíz e b está depois da raíz, ou seja, a raíz está no intervalo.
Inicialmente, o valor que definimos para a raíz R é o valor médio do intervalo [a,b], ou seja, (a+b)/2. Se esse valor satisfaz nossa necessidade, paramos, senão, continuamos até obter ruma maior precisão.
O algoritmo do método é o seguinte:
Listagem 1: algoritmo do método da bissecção
ENTRADA: Inicio, Fim: reais; Precisão, Iterações: inteiros;
VARIÁVEIS: Raiz, Erro, Temp: real;
INÍCIO
Erro = 1; //Definimos um erro muito grande para iniciar as iterações
Cont = 0;
ENQUANTO Erro > Precisão E Cont < Iterações
//Enquanto não obtivermos a precisão desejada ou enquanto não
//atingirmos um número máximo de iteações
Temp = Raiz; //Armazenamos o valor anteriormente encontrado
Raiz = (Inicio + Fim)/2;
Erro = ABS((Raiz - Temp)/Raiz);//Usamos o módulo (valor ABSoluto);
SE f(Inicio)*f(Raiz) < 0
//Se essa condição for verdadeira, implica dizer que a raiz está entre
//Inicio e Raiz (que é a metade do intervalo), o novo intervalo passa
//a ser [Inicio, Raiz] e dentro dele faremos novamente a verificação
Fim = Raiz;
SENÃO
//Senão, a raiz está no segundo subintervalo, e o intervalo passa a ser
//[Raiz, Fim] e dentro dele executaremos o processo novamente
Início = Raiz;
FIM_SE
Cont = Cont + 1;
//Esse contador é utilizado para fazer um controle do método.
//Se dentro de um número máximo de Iterações, não se obtiver um
//valor satisfatório, paramos
FIM_ENQUANTO
FIM
Agora vamos ao C#. Primeiramente definiremos nossa função f como já foi apresentado:
Listagem 2: função f da qual se busca a raiz
private double f(int t)
{
return 9 * Math.Exp(-1 * t) * Math.Cos(2 * Math.PI * t) - 3;
}
E então implementamos o método da bissecção:
Listagem 3: implementação do método da bissecção.
private double Bisseccao(double inicio, double fim, double precisao, int iteracoes)
{
double Erro = 1;
int Cont = 0;
double Raiz = inicio;
double Temp;
while (Erro > precisao && Cont < iteracoes)
{
Temp = Raiz;
Raiz = (inicio + fim) / 2;
Erro = Math.Abs((Raiz - Temp) / Raiz);
if (f(inicio) * f(Raiz) < 0)
fim = Raiz;
else
inicio = Raiz;
Cont++;
}
return Raiz;
}
Como conhecemos um intervalo inicial , podemos usar o método:
Listagem 4: utilizando o método da bissecção
double raiz = Bisseccao(0.1, 0.2, 0.001, 100);
No exemplo, utilizamos o intervalo inicial que encontramos observando o gráfico, [0.1, 0.2], e definimos uma precisão de 0.001, ou seja, não aceitamos um erro superior a isso. Determinamos, ainda, que o número máximo de iterações é 100.
Se executarmos os códigos acima, encontraremos uma raiz aproximadamente 0.1842, mas de fato esse valor não é exato. O C#, bem como outras linguagens de alto nível, não possui uma boa precisão para estes cálculos.
Vale lembrar, ainda, que a função f pode ser modificada, apenas utilizei um exemplo que achei interessante. E para encontrar o intervalo inicial, podemos plotar o gráfico e observar onde a curva intercepta o eixo X.
Bom, esse é apenas um dos métodos numéricos utilizados e é também o mais simples deles. Por hora ficaremos por aqui, espero que gostem.
Até a próxima.






