Grafos são utilizados para a solução de uma grande quantidade de problemas em computação como, por exemplo, representar o relacionamento de usuários em uma rede social, desenvolver algoritmos de roteamento em redes de computadores e a implementação de diversos algoritmos de logística (como a roteirização de veículos e a definição do melhor caminho).
Porém, desses problemas, diversos demandam enorme poder computacional, como achar a melhor sequência de cidades a serem percorridas ou decidir qual o usuário mais influente de uma rede social, ainda mais quando lidamos com Big Data.
Por isso é importante a existência de ferramentas que possibilitem a análise de grafos muito grandes. Pensando nisso, o Apache Spark disponibiliza o componente GraphX, recurso que viabiliza o processamento de algoritmos relacionados a grafos de forma paralela e distribuída.
O Spark tem ganhado bastante destaque nos últimos meses, se tornando, inclusive, o projeto da Apache que mais recebeu commits em 2015. Este resultado se deve principalmente ao excelente desempenho das aplicações escritas com essa ferramenta, que tem como objetivo processar grandes conjuntos de dados de forma paralela e distribuída.
O framework mais conhecido com esse propósito é o Hadoop, porém, testes mostram que o Spark possui um desempenho superior ao concorrente em diversas situações. Além disso, possui várias ferramentas que facilitam seu uso, como Spark SQL, Spark Streaming, MLlib e GraphX.
Um tipo de aplicação que pode ser tratado utilizando ferramentas Big Data são os grafos, teoria da Matemática comumente adotada para a solução de um grande número de problemas. Isso porque, se for viável modelar o problema em vértices (ou nós) e arestas (ou arcos), é possível fazer uso de todo o conhecimento já construído sobre esse conceito.
Pensando nisso, o Spark disponibiliza diversos algoritmos prontos para serem executados, tanto os clássicos de busca e distância, quanto os focados em problemas atuais, como a verificação de conexão entre usuários de redes sociais e o algoritmo de relevância de páginas criado pelo Google, o PageRank.
Visto que os algoritmos de grafos, tradicionalmente, dependem de grande poder computacional, o Spark também leva esse fato em consideração, sendo uma solução que pode ajudar no processamento de aplicações desse tipo através do uso do GraphX, um componente construído sobre o Spark Core que facilita a análise de grafos.
Como um dos seus diferenciais, o Spark é executado de forma paralela e distribuída, permitindo a escalabilidade das soluções, e isso com pouca ou nenhuma necessidade de alteração no código fonte da aplicação.
Para apresentar a utilização do GraphX, esse artigo trará a implementação de dois exemplos. O primeiro se preocupa em abordar conceitos básicos para mostrar um grafo com aeroportos e os voos entre eles, assim como ensinar como realizar alguns cálculos sobre o mesmo.
Esta solução será construída apenas em Scala, linguagem da API do GraphX. O segundo exemplo, por sua vez, terá o objetivo de simular uma rede social com usuários e suas conexões e também fará diversos processamentos sobre o grafo.
No entanto, terá parte do seu desenvolvimento em Java e parte em Scala, para demonstrar como integrar aplicações escritas nessas duas linguagens.
Teoria dos Grafos
Grafos é um conceito matemático muito popular em computação, pois muitos problemas do mundo real podem ser modelados com vértices (ou nós) e arestas.
Por causa disso, existem diversos algoritmos desenvolvidos sobre essa estrutura e que podem ser utilizados independente do domínio da aplicação. Por exemplo, o algoritmo de Dijkstra, um dos mais famosos, pode calcular a melhor rota entre dois roteadores na Internet, entre dois pontos em um mapa e também o custo do voo entre dois aeroportos sem nenhuma alteração em seu código.
A Figura 1 traz um exemplo de grafo que representa o caminho entre algumas cidades. Na imagem é possível perceber que de Lins existe um caminho direto para São Paulo ou Campinas. Porém, se você quiser ir para o Rio de Janeiro, deverá passar por uma dessas duas cidades.

Figura 1. Exemplo de grafo que mostra a conexão de estradas entre algumas cidades.
Atualmente, um dos principais exemplos da teoria dos grafos pode ser verificado na implementação de redes sociais, pois um grafo pode ser usado para modelar as pessoas e seus contatos em uma rede, qual usuário compartilhou uma postagem ou uma foto, entre muitas outras opções.
Através de outros algoritmos da teoria dos grafos, como a busca em largura ou a busca em profundidade, essas redes sociais conseguem calcular quantos amigos em comum duas pessoas têm, a distância em número de contatos que estamos de outras pessoas, entre outras possibilidades.
Porém, a teoria dos grafos tem um grande problema: normalmente os algoritmos são computacionalmente caros. Um exemplo é o algoritmo do caixeiro viajante, também conhecido como TSP (Travel Sales Problem), que consiste em decidir a melhor sequência de cidades que uma pessoa deve visitar, de forma a percorrer a menor distância possível. Esse algoritmo, até hoje, não possui uma solução ótima para grafos de qualquer tamanho.
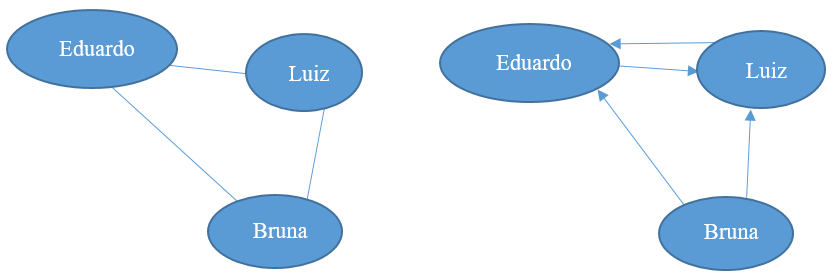
Em teoria dos grafos, uma questão importante é saber se as arestas dos grafos têm direção ou não. Isto porque em alguns grafos não existe orientação na aresta, ou seja, ambos os vértices que a aresta liga podem ser destino ou origem. Um exemplo onde isso acontece é em redes sociais como o Facebook, na qual não faz sentido ter orientação na aresta. Se duas pessoas estão conectadas na rede, não existe um usuário que é origem e outro que é destino.
Os usuários estão ligados da mesma forma. Por sua vez, em uma rede social como Twitter ou Instagram, os vértices precisam ser diferentes, visto que uma pessoa é o “seguidor” e a outra é o “seguido”. Neste caso, faz sentido ter a orientação no grafo para diferenciar o tipo de vértice e saber qual a relação entre eles.
Esse conceito é importante porque no GraphX todos os grafos são direcionados, isto é, todas as arestas têm uma orientação, um vértice de origem e um vértice de destino. A Figura 2 demonstra essas duas opções.
 ...
...