Artigo Java Magazine 26 - Números em Java

A manipulação de números é uma das características fundamentais de qualquer linguagem de programação. Como não poderia deixar de ser, Java fornece vários recursos avançados nesta área – mas devido a suas raízes orientadas a objetos o faz de modo diferente da maioria das outras linguagens.

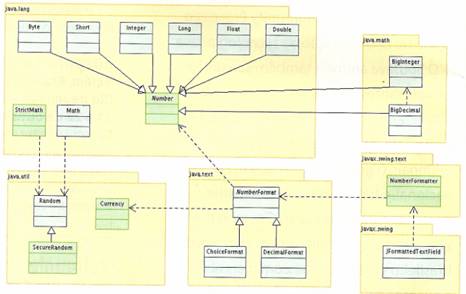
Este artigo apresenta as principais facilidades da linguagem Java e sua biblioteca padrão de classes para a manipulação de números – indo desde o básico até os recursos avançados como aritmética de precisão ilimitada e edição formatada. A Figura 1 ilustra as principais classes para a manipulação de números fornecidas com o J2SE (exceto pelas classes de exceções e de erros).

Na primeira parte, são apresentados fundamentos da manipulação de números por computadores, fornecendo ao leitor subsídios para escolher entre os vários tipos numéricos oferecidos por Java. Na segunda parte, são abordadas questões mais do dia-a-dia do programador, como a geração de números aleatórios e a formatação numérica.

 Figura 1. Diagrama UML com as principais classes e pacotes do J2SE 5.0 relacionados om números; as classes em azul são as mais comumentes utilizadas.

Tipos de dados numéricos

Os tipos de dados numéricos, independentemente da linguagem, podem ser divididos em quatro categorias:

1. Números inteiros. Não têm parte decimal (ou fracionária) e normalmente são manipulados diretamente pela CPU do computador.
2. Números em ponto flutuante. Possuem uma parte decimal ou fracionária; são manipulados diretamente por CPUs que incluam um co-processador numérico ou um componente equivalente; no arredondamento e precisão limitada.
3. Números em decimal-compactado. Não apresentam problemas de arredondamento, ou melhor, o fazem da forma como estamos habituados na representação decimal, e não na representação binária como é feito para números de ponto flutuante.
4. Números de precisão ilimitada. São manipulados por algoritmos baseados nos recursos de carry (vai-um) presentes em CPUs, para simular números maiores do que podem ser manipulados diretamente pelos processadores.

   Pensando em eficiência, queremos usar em nossos programas a menor quantidade possível de bytes capaz de armazenar um número. Por isso, as linguagens de programação modernas fornecem vários tipos de números inteiros ou de ponto flutuante, com variados graus de precisão. Quanto mais preciso for um número, mais extensa a faixa de valores que pode ser armazenada nele, e mair a quantidade de bytes ocupada.

Se possível, devem ser utilizados números inteiros, que são os mais eficientes em uso de CPU e memória. Caso se necessite de números com parte decimal, pode ser utilizada qualquer uma das outras categorias. Os números de ponto flutuante são os mais eficientes, entretanto eles não são indicados para lidar com valores monetários. Um dos motivos é porque a representação binária gera dízimas periódicas para alguns números com representação exata em decimal, podendo provocar erros de arredondamento. A Listagem 1 apresenta um exemplo deste problema (ao final desta e de outras listagens é demonstrada a execução e alguns resultados do exemplo).

A ciência já lidava com o problema do “erro” em valores numéricos bem antes dos computadores existirem, pois qualquer medição tem uma margem de erro. Então os valores nunca podem ser tomados como sendo exatos. No colégio, por exemplo, estudamos o conceito de “algarismos duvidosos” como uma das formas de a ciência lidar com erros.

Na maioria dos casos, práticas simples como evitar comparações de igualdade envolvendo números de ponto flutuante, ou fazer comparações dentro de uma “faixa aceitável”, evita os problemas. Por exemplo, em vez de testar se um números é igual a 0,5 poderíamos testar se ele está entre 0,49 e 0,51. ao invés de verificar se é maior ou igual a 7,0 tente averiguar se é maior ou igual a 0,65. a idéia é usar valores que poderiam ser arrendondados para o valore desejado.

Se estamos lidando com informações monetárias, é claro que ninguém ficará feliz com um “algarismo duvidoso” no saldo da conta bancária, nem com possíveis erros de arredondamento (para cima) em cálculos de taxas de juros. Para estes casos, precisamos de números com representação exata – que fazem parte das duas últimas categorias citadas.

O tipo BCD (Binary – Coded Decimal, ou “decimal compacto”) é comum em linguagens “orientadas a negócios” como COBOL e é implementado diretamente por algumas CPUs. Números em BCD utilizam múltiplos de 4bits (=um dígito decimal), não necessariamente múltiplos de 8 bits. É por isso que mainframes IBM usam grupos de 36 bits (e não de 32, como nos PCs). Note que o maior valor BCD armazenável numa certa quantidade de bytes é bem menor que o maior valor binário (inteiro) que pode ser armazenado no mesmo espaço. Por exemplo, em dois bytes o maior valor BCD possível é 9.999, enquanto que em binário é 32.767.

Os números de precisão ilimitada são geralmente implementados com arrays de inteiros e como listas encadeadas de inteiros. Se o número crescer, adiciona-se mais um inteiro ao array ou à lista. Toda aritmética é feita um inteiro por vez e é transferindo o “vai-um” (carry) para o próximo inteiro, da mesma forma que fazemos de um dígito para o outro nas contas em lápis e papel.

Listagem 1: Erro de arredondamento utilizando números de ponto flutuante           

public class PontoFlutuante {

   public static void main(String[] args) {

     System.out.println(“0.9 = 0.3 + 0.3 + 0.3 = ” + (0.3 + 0.3 + 0.3));

   }

}

$ java PontoFlutuante

0.9 = 0.3 + 0.3 + 0.3 = 0.8999999999999999

Tipos numéricos do Java

Java fornece tipos de dados inteiros, de ponto flutuante e de precisão ilimitada, mas não números BCD. Entretanto, a forma engenhosa como java utiliza aritmética sem erros de arredondamento.

Outras linguagens, como C e Pascal, deixam a definição da precisão, ou da quantidade de bytes de números inteiros e de ponto flutuante, a critério do compilador, o que torna complicada qualquer tentativa de programação portável ¹. Java, em vez disso, define exatamente o tamanho de cada tipo de dados numéricos, conforme a Tabela 1. nessa tabela, para sermos completos, também incluímos os tipos de precisão ilimitada, para que todos os tipos numéricos do Java estejam presentes.

Note que Java não se define inteiros sem sinal, como feito por C. Por isso o maior valor de uma variável do tipo byte é 127 e não 256, pois há também os números negativos. O mesmo vale para short, int e long.

Os números de precisão ilimitada do Java será vistos com mais detalhes adiante. Para detalhes sobre os números de ponto flutuante do Java, consulte o artigo “Matemática em Java” na Edição 19.

Observe que o tipo java.til.Currency não representa um valor monetário, e sim o identificador de moeda das configurações regionais; por exemplo “R$”.