Distribuição Binomial em Java

1. Introdução

Imagine que um programador esteja criando um joguinho para telefone celular em que o objetivo seja comandar um foguete em uma viagem até Marte, sendo necessário para isso ultrapassar uma sequência de n naves espaciais que se encontram a sua frente (ex: 30 naves). Cada nave a ser ultrapassada pode ser de apenas um dos seguintes dois tipos:

• nave marciana (M): é a nave inimiga. Quando o foguete do jogador se deparar com esse tipo de nave, será preciso duelar. A nave marciana vai atirar e tentará derrubá-lo; por isso, o foguete só poderá ultrapassá-la, se contra-atacar e conseguir derrubá-la.
• nave neutra (~M): neste caso, não se trata de uma nave inimiga e o jogador deverá apenas ultrapassá-la. Caso o jogador se confunda e atire em uma nave neutra, perderá o jogo! (obs: a representação ~M escolhida para a nave neutra significa “não marciana”).

Considere que o programador deste joguinho tenha decidido que na primeira fase, o objetivo seja ultrapassar uma sequência de 30 naves. Para dar mais dificuldade ao jogo, ele quer que cada nave que surja na sequência tenha 80% de chance de ser uma nave marciana e apenas 20% de chance de ser uma nave neutra.

Nesse caso, como ele poderia criar um procedimento para produzir diferentes sequências aleatórias com essas características? Ou seja: como desenvolver um gerador de sequências não fixas de naves que sejam compostas por aproximadamente 80% de naves M e 20% de naves ~M? Felizmente (para o programador do joguinho!), o problema acima pode ser resolvido de maneira simples, pois a sequência de naves espaciais que será produzida possui distribuição binomial probabilidades. Trata-se de uma das mais conhecidas distribuições de probabilidade e uma das que possui o maior número de aplicações práticas. Este artigo tem dois objetivos: introduzir os conceitos básicos sobre distribuição binomial de probabilidades e apresentar uma técnica para trabalhar com este tipo de distribuição na linguagem Java.

2. A Distribuição Binomial

Antes de abordarmos a implementação Java, apresentamos nesta seção uma breve definição formal para distribuição binomial de probabilidades, para que o leitor fique familiarizado com os seus principais conceitos e características.

• Considere um experimento E e seja M um evento associado a E.
• Seja P(M) = p (a probabilidade de ocorrência do evento M é p). Sendo assim, temos P(~M) = 1 – p (probabilidade de não ocorrer o evento M).
• Considere que sejam realizadas n repetições do experimento. Dessa forma, o conjunto de todos os resultados possíveis para o experimento (espaço amostral) será formado por todas as sequências possíveis {m1, m2, ..., Mn}, onde cada elemento dentro da sequência é M ou ~M. Por exemplo, considerando n=3, o conjunto com todos os resultados possíveis é dado por:
  {M,M,M}
  {M,M,~M}
  {M,~M,M}
  {M,~M,~M}
  {~M,M,M}
  {~M,M,~M}
  {~M,~M,M}
  {~M,~M,~M}
• Suponha que P(M) = p seja sempre a mesma para todas as repetições.
• Seja a variável (aleatória) X = {número de vezes que o evento M tenha ocorrido na sequência de n repetições}. Dizemos que X possui distribuição binomial com parâmetros n e p.

O exemplo do joguinho da sequência de 30 naves marcianas e naves neutras apresentado na seção anterior se enquadra exatamente nesse caso. Neste caso, estamos lidando com o seguinte fenômeno (variável aleatória): X = “número de vezes em que a nave marciana aparece em uma sequência”. Veja que X é claramente uma variável com distribuição binomial, cujos parâmetros são n=30 (tamanho da sequência) e p = 0,80 (probabilidade de uma nave ser marciana).

3. Implementação Java

A Listagem 1 mostra o código Java com a definição da classe “DistribuicaoBinomial”. Esta classe possui um método estático chamado “gerarSequencia” responsável por gerar uma sequencia com distribuição binomial a partir dos parâmetros n e p. A sequência produzida é armazenada em um vetor binário e retornada ao usuário. A explicação detalhada é apresentada em seguida ao código.

Listagem 1: Classe “DistribuicaoBinomial”

public class DistribuicaoBinomial {

	/**
	 * gera uma sequência com distribuição binomial com parâmetros n e p
	 * @param n número de repetições
	 * @param p probabilidade de sucesso do evento
	 * @return vetor binário contendo a sequência gerada
	 */
	 public static int [] gerarSequencia(int n, double p) {
	        
		 //PASSO 1. reserva memória para o vetor que será retornado 
		 int [] vet = new int[n]; 
		 
		 //PASSO 2. loop que preenche cada posição do vetor
		 for(int i = 0; i < n; i++) {
			 vet[i] = (Math.random() < p) ? 1 : 0;
		 }
         
		 //PASSO 3. retorna o vetor
		 return vet;
	 }
  
}
 

O método “gerarSequencia” produzirá como saída sempre um vetor binário de tamanho n. Por exemplo, considerando n=30 e p=0,80, um exemplo de vetor que poderia ser produzido pelo método é dado abaixo:

111111111001111111111001011111

Os valores “1” representam a ocorrência do evento M (neste caso, associado a probabilidade p=0,80) enquanto os valores “0” representam a não ocorrência de M (ou ~M). Retornando ao exemplo das naves espaciais, a sequência acima estaria representando a seguinte situação:

• Primeiro, o foguete do jogador enfrentaria 9 naves marcianas em sequência.
• Depois viriam 2 naves neutras para ultrapassar.
• Depois mais 10 naves marcianas a serem enfrentadas.
• Finalizando a sequência: 2 neutras, 1 marciana, 1 neutra e 5 marcianas.

É importante destacar que as sequências são produzidas sempre de maneira aleatória, considerando os parâmetros n e p. A explicação sobre o programa é dada a seguir.

Inicialmente, o programa aloca em memória um vetor de inteiros de tamanho n (PASSO 1). Depois, temos o PASSO 2 que é o principal do método. Nele, é realizado um loop que sorteia o valor de cada posição do vetor (sempre 1 ou 0). Este sorteio é feito levando em consideração o valor de p, ou seja, levando em consideração a probabilidade de que o valor 1 seja sorteado. Para conseguir que isso fosse possível, o artifício empregado foi utilizar o método “random()” da classe “Math”:

vet[i] = (Math.random() < p) ? 1 : 0;

“Math.random()” sorteia um número entre 0 e 1, considerando uma distribuição uniforme nesse intervalo. Isso quer dizer que qualquer número real (double) maior ou igual a 0.0 e menor que 1.0 pode ser sorteado com a mesma probabilidade. Desta forma, basta chamar “Math.random()” dentro de cada iteração i do loop e verificar se o número sorteado é menor do que o parâmetro p (ex: menor do que 0,80). Se isto for verdade, v[i] receberá 1. Se for falso, v[i] receberá 0. Após o loop se encerrar, um ponteiro para o vetor “v” é retornado pelo método (PASSO 3).

Para testar o programa, você pode utilizar o programa da Listagem 2. Neste exemplo, são geradas três sequências, representadas nos vetores v1, v2 e v3, respectivamente. Para v1, usamos os parâmetros n=3 e p=0,66. Para v2, temos n=10 e p=0,25. E finalmente para v3, temos a situação que representa o exemplo do jogo das naves espaciais, onde n=30 (sequência de 30 naves espaciais) e p = 0,80 (probabilidade de uma nave ser marciana).

Listagem 2: Testando a Classe “DistribuicaoBinomial”

public class TestaDistribuicaoBinomial {

	public static void main(String[] args) {
		
		int v1[], v2[], v3[];
		
		//gera sequência com n = 3 e p = 0,66. Armazena em v1
		v1 = DistribuicaoBinomial.gerarSequencia(3, 0.66);
		
		for (int i=0; i < 3; i++) System.out.print(v1[i]); //imprime v1
		System.out.println();

		
		//gera sequência com n = 10 e p = 0,25. Armazena em v2
		v2 = DistribuicaoBinomial.gerarSequencia(10, 0.25);
		
		for (int i=0; i < 10; i++) System.out.print(v2[i]); //imprime v2
		System.out.println();

		//gera sequência com n = 30 e p = 0,80. Armazena em v3
		v3 = DistribuicaoBinomial.gerarSequencia(30, 0.80);
		
		for (int i=0; i < 30; i++) System.out.print(v3[i]); //imprime v3
		System.out.println();
		
	}
	
}
 

Um exemplo de resultado possível é apresentado na Figura 1.

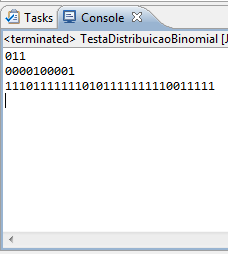
Figura 1: Execução do programa da Listagem 2

É importante deixar claro que as sequências são sempre geradas de forma aleatória, porém de acordo com uma distribuição binomial com parâmetros n e p. A cada execução do programa, uma diferente sequência deverá ser gerada. Se o valor de p for alto, a tendência é que a sequência possua muitos 1’s (como é o caso de v3) e se for baixo, a tendência é que existam mais zeros (caso de v2).

Quando, por exemplo, especificamos p=0,80 e n=30 isso não significa que exatamente 80% dos valores do vetor gerado terão o valor 1 (24 posições). Na verdade, o que ocorre é que para cada posição do vetor, a chance de 1 ser sorteado estará associada a uma probabilidade de 80%. Tipicamente, o total de 1’s das sequências variará nas diferentes chamadas do método “gerarSequencia”. No entanto, se executarmos um grande número de chamadas ao método, poderemos verificar que, em média, o total de 1’s estará próximo de 24 (embora cada sequência individual não possua sempre 24 valores 1).