Com estas ferramentas e com o auxílio do Hibernate Spatial, veremos como se torna muito mais simples a tarefa de desenvolver uma aplicação capaz de persistir e consultar dados baseados em coordenadas de um sistema geográfico, para posteriormente exibi-los, por exemplo, no Google Maps.
Por volta do ano 2008, aplicativos que fazem uso de dados de localização espacial utilizando recursos do Sistema de Posicionamento Global (GPS), combinados com tecnologias de transferência de dados (3G), começaram a surgir de forma tímida em dispositivos móveis, sendo o FourSquare uma das primeiras apps a alavancar o uso dessas tecnologias.
Hoje, apenas seis anos após o lançamento do iPhone 3G e do FourSquare, é praticamente incontável o número de aplicativos baseados no uso de posicionamento, tentando fazer com que este tipo de serviço revele-se um grande diferencial na experiência do usuário final.
Como as possibilidades de se oferecer informações baseadas em posicionamento são praticamente ilimitadas, os aplicativos que lidam com localização espacial tendem a se especializar com o objetivo de responder com eficiência um pequeno conjunto de perguntas, relacionadas a categorias de objetos georreferenciados bem definidas, que no geral podem ser resumidas a: “Dada uma posição P, quais são os objetos de determinada categoria de meu interesse mais próximos?”.
Estas categorias podem ser lojas, amigos, bares, enfim, qualquer coisa que esteja situada entre a superfície e a exosfera da Terra!
Outro benefício oferecido por tecnologias de localização é a sinergia, ou seja, a capacidade de se combinar com recursos já existentes de uma aplicação de forma a oferecer uma experiência superior ao usuário final.
A inclusão da informação de posicionamento pode melhorar desde os mais simples detalhes de sistemas, como “descobrir” o idioma a ser utilizado baseado no local em que o programa é executado, como vir a ser a funcionalidade central dos mesmos.
O sucesso de muitos aplicativos baseados em crowd sourcing, como o Waze, onde os usuários são os principais responsáveis por alimentar os dados do sistema, se deve à qualidade da harmonização dos dados de posicionamento geográfico com as outras fontes de informação.
Neste artigo vamos estudar os principais conceitos envolvidos para desenvolver aplicações com georreferenciamento em Java, iniciando pelos fundamentos de Geometria da Java Topology Suite, a qual permite realizar operações com pontos, linhas e polígonos em um plano cartesiano, passando por breves noções de cartografia do GeoTools, que dá a capacidade de trabalhar com informações de posicionamento reais sobre o globo terrestre, e finalmente veremos como é simples persistir e consultar estes tipos de dados a partir do Hibernate Spatial.
Java Topology Suite (JTS)
A API Java Topology Suite foi a primeira biblioteca escrita em Java para lidar com formas geométricas, estando disponível desde 2002. As classes contidas no JTS permitem a construção de objetos que representam Pontos, Linhas e Polígonos, e também proveem dezenas de métodos para lidar com operações de geometria, como intersecção e cálculo de distância.
O JTS define Geometria como uma coleção de Coordenadas, que por sua vez podem ser pensadas como pontos em um sistema de coordenadas cartesiano. A hierarquia das classes fundamentais do JTS é ilustrada no diagrama da Figura 1 e o significado de cada componente do mesmo está elencado logo a seguir:
· Geometry (Geometria): Classe que define uma geometria como sendo uma sequência de coordenadas e operações. Esta classe declara um atributo chamado SRID (Spatial Reference System Id), que não é utilizado pela API do JTS e sim por extensões espaciais de bancos de dados, como veremos mais à frente;
· Point (Ponto): uma única coordenada no espaço;
· LineString (Linha): coleção de duas ou mais coordenadas. Linhas definem o conceito de comprimento, que pode ser calculado pela soma da distância de cada par de segmentos que a compõe. Por exemplo, se a linha for formada por três coordenadas (A, B e C) o comprimento da linha é a distância do segmento (A, B) somada à distância do segmento (B, C);
· LinearRing (Anel): Anéis são linhas fechadas, ou seja, linhas cuja última coordenada é idêntica à primeira;
· Polygon (Polígono): um polígono é definido como um LinearRing exterior, chamado de casca (shell) ou fronteira, e pode conter N buracos (holes), que por sua vez também são anéis, mas que estão ausentes na composição do polígono.
Polígonos definem o conceito de área, que é calculada como sendo a área total da região representada pela fronteira, subtraída da área representada pelos buracos. Por exemplo, a área do polígono representado na Figura 2 é a área do quadrado menos a área dos três buracos (triângulo, círculo e octógono);
· GeometryCollection: união de diferentes geometrias;
· GeometryFactory: Classe utilitária para criar geometrias e necessária para realizar algumas operações geométricas. Embora geometrias possam ser instanciadas diretamente, como boa prática elas devem ser criadas a partir dos métodos de GeometryFactory, de modo que fiquem corretamente associada à instância da mesma e com o valor de SRID equivalente;
· GeometricShapeFactory: O JTS não permite criar linhas com curvatura, ou seja, a princípio não é possível descrever formas como círculos e elipses. Entretanto, esta classe utilitária permite criar polígonos similares a estas formas curvas, as quais podem ser pensadas como sendo coleções de pequenos segmentos de reta.
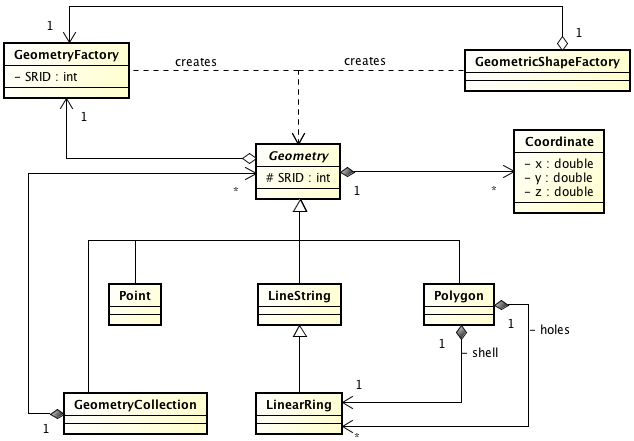
Figura 1. Fábricas e Hierarquia das classes do JTS.
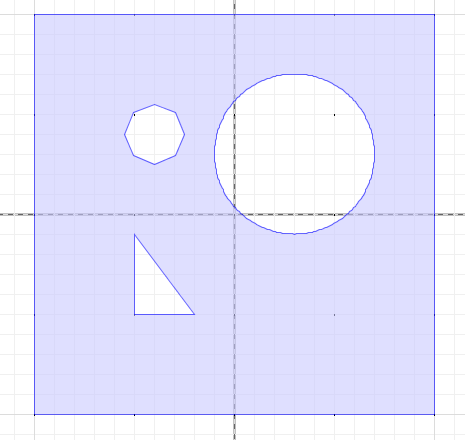
Figura 2. Polígono com buracos.
Criando e testando geometrias
Um polígono como o mostrado na Figura 2 pode ser facilmente construído de maneira programática, a partir de arrays de coordenadas e métodos de GeometryFactory e GeometricShapeFactory.
O código apresentado na Listagem 1 demonstra como estas classes são empregadas para produzir diferentes formas geométricas. Nesta listagem, o método createCircleAround() é utilizado para gerar as “circunferências” dentro do quadrado da Figura 2. Note que no JTS, círculos são, na realidade, aproximações de polígonos com N vértices equidistantes a partir de um ponto de referência.
Se utilizarmos poucos pontos, como no caso do polígono no segundo quadrante, que foi criado com apenas oito vértices, não teremos a “impressão” de curvatura, como ocorre com a circunferência grande, que utilizou 64 vértices.
Para verificar algumas funcionalidades do JTS, apresentamos o código testPolygon() da Listagem 1, no qual são criados dois quadrados de lado 2, um cheio e outro com buracos, como o da Figura 2. Ao empregar o método getArea() da classe Polygon, podemos verificar que o quadrado cheio apresenta o resultado esperado (área=2x2) e que de fato o quadrado com furos possui área inferior ao quadrado cheio.
Listagem 1. Testando a API do JTS.
public class TestJTS {
GeometryFactory factory = new GeometryFactory();
/**
* Utilitário para criar Coordenada
*/
static Coordinate c(double x,double y){
return new Coordinate(x,y);
}
/**
* Utilitário para aproximar um círculo por um número finito de coordenadas.
*
* @param origin - centro do círculo
* @param radius - raio da circunferência
* @param vertexes - número de vértices
*/
private Polygon createCircleAround(Coordinate origin, double radius,
int vertexes) throws TransformException {
GeometricShapeFactory gsf = new GeometricShapeFactory(factory);
gsf.setCentre(origin);
gsf.setWidth(radius*2);
gsf.setHeight(radius*2);
//Mínimo de 5 vértices
gsf.setNumPoints(vertexes>4?vertexes:32);
return gsf.createCircle();
}
@Test
public void testPolygon() throws TransformException{
//Coordenadas de um quadrado com lado 2
Coordinate[] squareCoords = new Coordinate[] { c(-1, -1), c(-1, 1),
c(1, 1), c(1, -1), c(-1, -1) };
LinearRing shell = factory.createLinearRing(squareCoords);
LinearRing triangle = factory.createLinearRing(new Coordinate[]{
c(-.5,-.5),c(-.2,-.5),c(-.5,-.1),c(-.5,-.5)});
LinearRing[] holes = new LinearRing[]{
triangle,
(LinearRing) createCircleAround(c(.3,.3), .4, 64).getExteriorRing(),
(LinearRing) createCircleAround(c(-.4,.4), .2, 8).getExteriorRing()
};
Polygon square = factory.createPolygon(shell);
Polygon squareWithHoles = factory.createPolygon(shell, holes);
//Verifica área do quadrado de lado com tamanho 2, com precisão de .000001
Assert.assertEquals(square.getArea(),4,.000001);
//Verifica que a área do quadrado cheio é superior à área do quadrado com buracos
Assert.assertTrue(square.getArea() > squareWithHoles.getArea());
}
}
...