1. Introdução
“Torres de Hanói” é um jogo matemático onde dispomos de 3 pinos: “pino origem”, “pino de trabalho” e “pino destino”. O “pino origem” contém n discos empilhados por ordem crescente de tamanho (o maior disco fica embaixo). O objetivo do jogo é levar todos os discos do “pino origem” para o “pino destino”, utilizando o “pino de trabalho” para auxiliar a tarefa, e atendendo às seguintes restrições:1. Apenas um disco pode ser movido por vez (o disco que estiver no topo da pilha de um dos pinos).
2. Um disco de tamanho maior nunca pode ser colocado sobre um disco de tamanho menor.
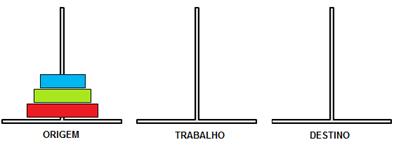
Figura 1.
A figura acima mostra um exemplo do jogo com 3 discos (azul, verde e vermelho), ou seja, com n = 3. É bastante comum encontrarmos o jogo das Torres de Hanói em museus de ciência para que visitantes adultos e crianças possam tentar solucioná-lo (normalmente os pinos e discos são confeccionados de madeira). Também existem diversos sites na Internet que disponibilizam a versão digital para ser jogada, como por exemplo: http://www.mathsisfun.com/games/towerofhanoi.html.
2. Solução Recursiva
O jogo das Torres de Hanói também é muito apreciado por programadores e cientistas da computação porque possui uma solução recursiva que pode ser programada de uma maneira muito simples e elegante.Como toda solução recursiva, ela baseia-se na resolução de um problema de menor dimensão (ou seja, na resolução de um problema como um menor número de discos). Para resolver um jogo onde precisamos mover n discos, considerando n > 1, podemos executar os seguintes passos:
· Mover n-1 discos para o “pino de trabalho”.
· Mover o n-ésimo pino (o maior de todos) do “pino origem” para o “pino destino”.
· Após isto, devemos resolver o problema da “Torre de Hanói” para os n-1 discos dispostos no “pino de trabalho”, movendo-os para o “pino destino” utilizando o mesmo princípio.
As figuras a seguir ilustram a solução, apresentando sequência de movimentos efetuados, considerando um jogo com 3 discos (n = 3):
PASSO 1
: Os movimentos 1, 2 e 3 mostram a transferência de n-1 discos do “pino origem” para o “pino de trabalho. Nesta caso, “pino destino” atua como auxiliar.Movimento 1
: Origem->Destino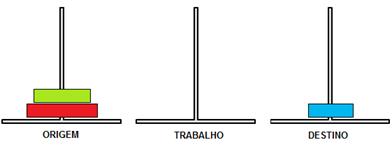
Figura 2.
Movimento 2:
Origem->Trabalho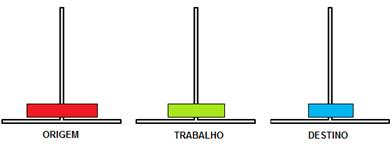
Figura 3.
Movimento 3
: Destino->Trabalho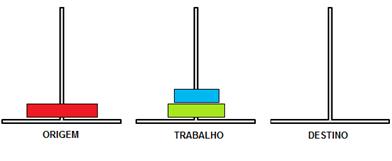
Figura 4.
PASSO 2
: O movimento 4 mostra a transferência do maior disco do “pino origem” para o “pino destino”Movimento 4
: Origem->Destino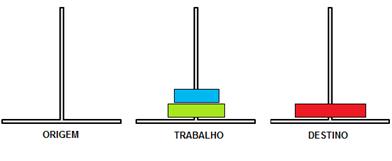
Figura 5.
PASSO 3
: Por fim, os movimentos 5, 6 e 7 ilustram a transferência dos n-1 discos do “pino de trabalho” para o “pino destino”. Veja que, desta vez, o “pino de origem” é que atua como área de armazenamento auxiliar.Movimento 5
: Trabalho->Origem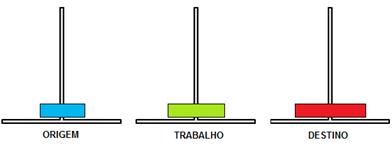
Figura 6.
Movimento 6
: Trabalho->Destino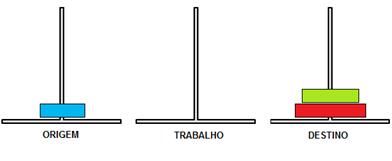
Figura 7.
Movimento 7
: Origem->Destino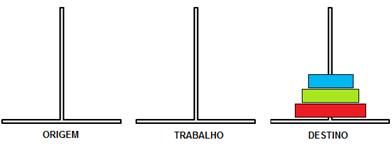
Figura 8.
3. Solução Recursiva em Java
A seguir, apresenta-se uma implementação da resolução recursiva do problema das Torres de Hanói na linguagem Java. O programa recebe como entrada o número de discos (valor de n) e, como saída, gera a sequência de movimentos necessários para resolver o problema. Nesta saída, os valores 1, 2 e 3 correspondem, respectivamente, aos pinos “origem”, “trabalho” e “destino”. Por exemplo: o valor 1->3 significa um movimento do “pino de origem” para o “pino destino”. Execute o programa com diferentes valores para o parâmetro n, tais como, 3, 5, 8, etc. Você verá que o número de movimentos cresce exponencialmente com o aumento do número de discos (a discussão sobre complexidade será apresentada no próximo artigo).
import java.util.Scanner;
public class TorresDeHanoi {
// Método que realiza (imprime) o movimento
// de um disco entre dois pinos
private static void mover(int O, int D) {
System.out.println(O + " -> " + D);
}
// Método que implementa a recursão
// O = pino origem
// D = pino destino
// T = pino de trabalho
static void hanoi(int n, int O, int D, int T) {
if (n > 0) {
hanoi(n - 1, O, T, D);
mover(O, D);
hanoi(n - 1, T, D, O);
}
}
// executando o hanoi
public static void main(String[] args) {
int n; // número de discos
// recebe o número de discos digitado pelo usuário
Scanner entrada = new Scanner(System.in);
System.out.println("Digite o número de discos: ");
n = entrada.nextInt();
// executa o hanoi!
TorresDeHanoi.hanoi(n, 1, 3, 2);
}
}